Hands-On Explorations: Math (Geometry with Straws)

Following up on the theme of actually schooling at home, rather than just hanging around the house cooking, cleaning, and letting the kids run around outside like savages, which is what we’ve done a lot of lately…

Yesterday, we did a quick, fun hands-on exploration of geometry which the kids sort of got into… though it’s not as easy as it looks.  The JUMP Math (Grade 2) book said to use straws, but honestly, straws are tough to work with because they’re flimsy and bend when you don’t want them to.  Popsicle sticks or skewers cut in half might be better, because they’re more rigid.

Basically, you start with plasticine balls (about the size of an olive) and create a 2-d shape…

Then “extrapolate” it into 3-d…

   

Mine was a pentagon, but Naomi’s 2-d shape was a square.  She grudgingly made a pyramid because I asked her to do that first, but what she really wanted was to make a cube…

The cube was frustrating because she insisted on using ONLY pink plasticine, and we didn’t have very much of it left, so the balls at the corner were too tiny to hold the straws in place very well.  I did eventually manage to get it built.  I thought “prismifying” our shapes was such a good idea that I took off the top of my pyramid to create a pentagonal prism:

Gavriel Zev, meanwhile, quickly gave up the straws to create…

   

Monsieur l’Escargot!  (but hey, aren’t spirals math, too???)

Before we got back to the book exercise that correlated with the straw-building, I used the opportunity to review some of the terminology, since this was actually the last page of the geometry strand.  We went over words like VERTEX, VERTICES, EDGE, FACE, plus the names of certain very basic 2-d polygons (SQUARE, CUBE, TRIANGLE, RECTANGLE, PENTAGON) and 3-d shapes (PYRAMID, CUBE, PRISM).  It was also a good, concrete introduction to the concept of dimensionality.

Speaking of which, although Naomi was later able to translate her 3-d straw-building skills to the 2-d page easily enough, another workbook page caused no end of difficulty.  In attempting to introduce the concept of counting edges, the 2-d representations of 3-d shapes were so complicated that she repeatedly missed edges on four illustrations out of five.  Very big frown for a book which has otherwise been pretty excellent for our learning styles.

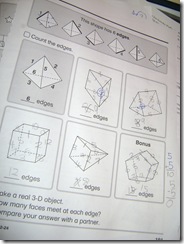
I was particularly discouraged by this page, however, because I saw it as a perfect opportunity to teach what John Mighton emphasizes about helping kids understand the importance of systematic search techniques.  If you’re counting sides of an object, wouldn’t it be helpful to introduce the idea of doing it “in order” rather than just willy-nilly? 

I gave up on the page and helped her through this a bit with REAL geometric solids, showing her that with, say, a triangular prism, you can count all the sides on ONE triangular end (so you get 3, and write it down), then flip it and count the OTHER triangular end (another 3, which you write down).  But of course, you’re not done because there are the edges in between both of those ends – write down another 3.  Then, you have a nice neat stack of 3’s, which is easy to add up (she had the answer long before I asked her to figure it out).

Using the plastic geometric solids meant I could also take a (washable) marker and show her that you can mark each side as you count it, so you don’t repeat yourself.  This is kindergarten-level stuff, but I figured she’d gotten so muddled by these dashed-lines-crossing diagrams that it was worth showing her it really DID make sense.

I am guessing this particular workbook page was included to meet various provincial curriculum standards, and I do understand that it is accompanied by a very concrete, hands-on lesson… but the fact is, representing 3-d shapes in 2 dimensions is confusing even to adults, and I’m not sure what value is added by making kids in grade 2, with little perspective-drawing experience, do it on paper. In retrospect, I probably should have skipped it.

To wrap this up on a positive note and fully concretize the lesson that two two-dimensional faces meet to form an edge (and create a 3-d shape), I cut out two triangles and three rectangles and had her tape them into a simple triangular prism.  You can find all sorts of print-and-fold nets for prisms and other 3-d shapes online (ooh, here’s a free printable Angry Birds version!), but I wanted one that was created from simple unconnected 2-d shapes.  Forgot to take a picture, but it wasn’t that awesome, just a happy way to finish this off.

It feels weird to be wrapping up the “year,” watching our math book get thinner and thinner (I tear out 2 pages each day for us to work through), but also nice to see how ready she is to begin the Grade 3 book, which looks scarily more “grown-up” than the Grade 1 and Grade 2 work.  The print is smaller, with fewer pictures and more exercises per page. 

I got lots of ideas at the JUMP workshop I attended over the summer… including the very important concept that she won’t have to complete every single problem on the page.  I knew this already, of course, but the instructor’s suggestion of making sure she could do the first few, then jumping to the end is probably a better solution than alternating problems all the way down the page, which would have been my instinct.  It will be a fun challenge, I think, to keep finding concrete approaches to the math at this level without dumbing it down or making it seem “babyish.”

How’s your math coming along so far this year?  Any breakthroughs?  Or are you happy enough with the same old…?